
It's a common misconception that the shorter a lens, the more distortion the image will receive. And while this may seem like what happens based on what we see, the simple fact remains that it is the object's relationship to the field of view that affects the final representation in the camera.
If we can assume an object to extend out beyond it's edge on a plane lying perpendicular to the camera lens we can extrapolate the size of that object's plane in relationship to the field of view and further express that as a percentage of the camera's frame.
Basically, at any given distance from the camera we want to find out how long of a length is covered perpendicular to the lens. We can then use that information to determine the percentage that a given object has in relation to the fame size.
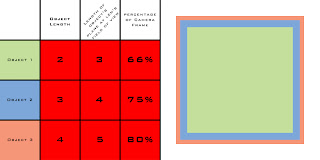
In the above diagram there are 4 "cameras" and 3 "objects". The red camera and the blue camera share the same field of view but a different position. The charts below show the effective size and the percentages of each of the objects in relationship to that specific camera's field of view.
The important thing to note is that while the objects remain stationary and their lengths unchanged, the relationship they exhibit to one another changes in a scalar form as the distance between the object and the lens changes. This is most apparent with the red and blue cameras which both share the same angular field of view with only a change in the distance from the objects.
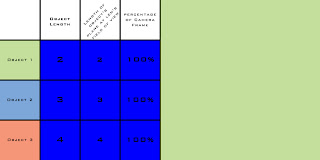
As we move our position (the camera) from the position of the red camera to the position of the blue camera the difference in relationship of each of the objects to the field of view changes until eventually each of the objects has a 100% of the frame's size in which each object overlaps the one behind them totally.
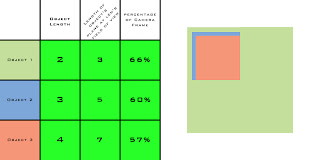
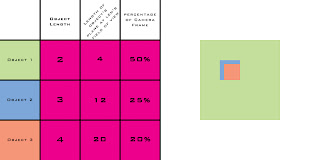
Continuing on, as we approach the green and subsequently the purple camera positions the effect of each object in relationship to each other continues until we reach the point where the difference in each field of view becomes greatly distorted. At the point we reach the position of the purple camera the 2nd object which is 150% the size of the first object becomes distorted to appear to be half the size (or thinking of it in reverse, the smaller object appears twice as large as the (in reality) larger object.
This happens simply because the object fills less of the frame since it's relationship to the field of view represents a smaller percentage within the total coverage for an object at that distance.
(it should be noted that the view's for the green and purple camera's have a cut out in the top left 1/4 of the first object to show where the subsequent objects would fall in relationship. The blue and red cameras both show a representation of how the objects would stack normally)




What we can get from this is that in order for an object of the same size to fill the same amount of space in the camera's frame we must use a wider lens as we move closer and a longer lens as we move away. In fact, both the red camera and the green camera represent object 1 as 66% of the frame. This is evidenced by both the charts as well as the first diagram where the intersection of object 1's plane is shared by both the red camera and the green camera's field of view.
An interesting change in the relationship happens however if we were to move the purple camera to the position of the red camera (a distance 6 times as far). If we move the purple camera object one will fill 0.083 percent of the frame, object 2 0.093 percent, and object 3 0.1 percent of the frame. The reason this is interesting is that the relationship of the sizes of each object remains roughly equivalent. 66% is 83% of 80%, whereas 0.083% is 83% of 0.1%, therefore the relationship of objects at any distance remains roughly equivalent at any given field of view.
